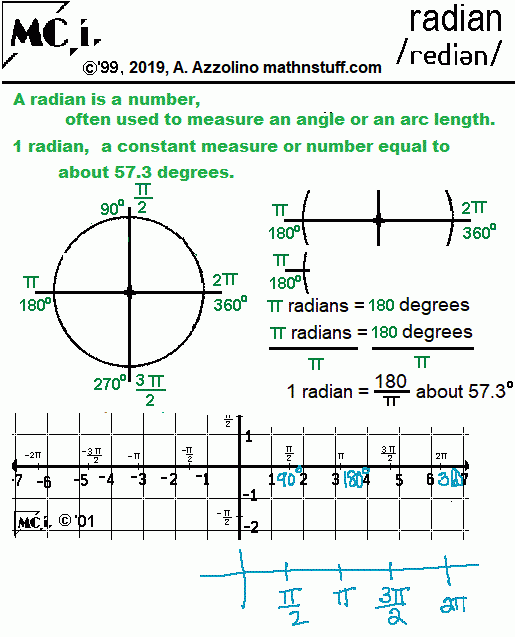
Understanding coterminal angles in both degrees and radians is an important concept in trigonometry. Coterminal angles are angles that have the same initial and terminal sides but differ by a multiple of 360 degrees (or 2π radians). This concept is crucial in various trigonometric calculations and conversions.
One way to practice and test your understanding of coterminal angles is through a worksheet. A coterminal angles degree and radian worksheet typically consists of several problems where you are given an angle in either degrees or radians and asked to find coterminal angles that differ by a multiple of 360 degrees or 2π radians.
 Worksheet 8 Radian And Degree Measures For Angles Draw An (www.yumpu.com)
Worksheet 8 Radian And Degree Measures For Angles Draw An (www.yumpu.com)
When working on a coterminal angles worksheet, it is important to remember that there are infinitely many coterminal angles for any given angle. To find coterminal angles, you can add or subtract 360 degrees (or 2π radians) to the given angle multiple times until you reach a new angle within the desired range.
It is also helpful to convert between degrees and radians when working on coterminal angle problems. Remember that 360 degrees is equivalent to 2π radians, so you can easily convert between the two units of measurement. This conversion is crucial for accurately determining coterminal angles in both degrees and radians.
Additionally, practicing with coterminal angles worksheets can help reinforce your understanding of trigonometric concepts such as periodicity and angle measurements. By working through various problems and finding coterminal angles, you can improve your problem-solving skills and gain confidence in your trigonometry abilities.
Overall, coterminal angles degree and radian worksheets are valuable tools for practicing and mastering trigonometric concepts related to angle measurements. By working through these worksheets and practicing finding coterminal angles, you can enhance your understanding of trigonometry and improve your problem-solving skills in this area of mathematics.